为什么深度学习是非参数的
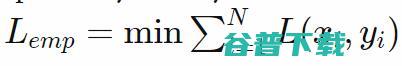最小化。如果我们的损失函数是负对数似然，将
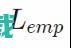最最小化就意味着计算最大相似估计。
对偏差-方差分解和偏差-方差平衡的简单介绍
中采得的随机变量，且我们训练的模型
f依赖于
D，记作
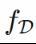
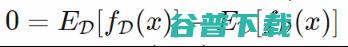并利用(,)和D的独立性，我们可以将预测的期望平方误差分解为：
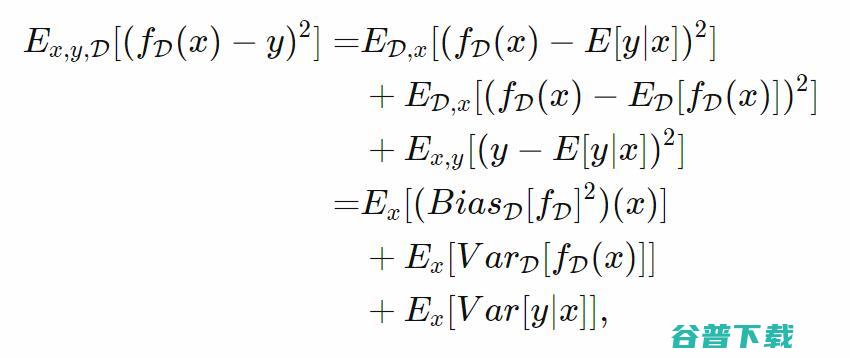
，我们可以让方差为0，这样则是极端的欠拟合。
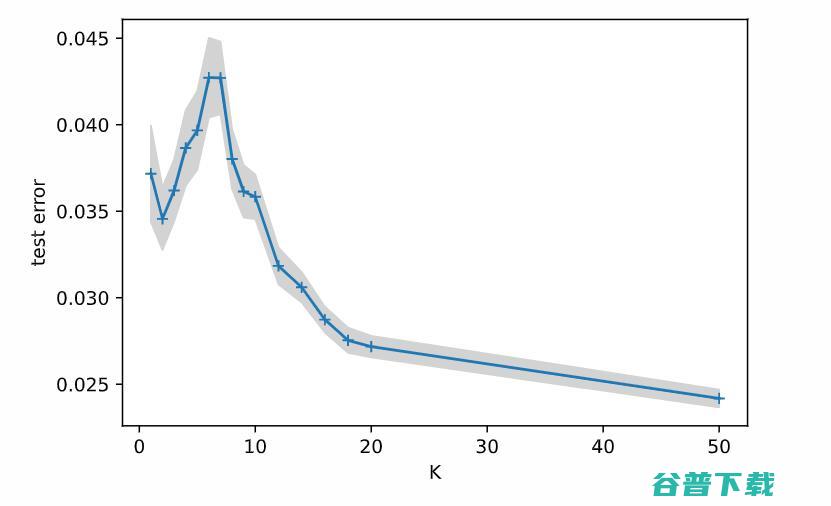
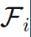的大小或其VC维的项。此处的典型情况是，一个人想要≥VC-dim个样本，却可能有≤20VC-dim个样本。但请注意，这里参数的数量不是标准的一部分(但可能会影响VC维)。
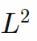里有弱导数的索伯列夫函数空间
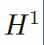(无论采用何种测度，是x的分布抑或是包含输入的
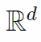的勒贝格测度)，我们可以匹配任意有限样本D上每一点的样本均值，从而可以获得0点态偏差, 但是最小化经验风险是病态的，有无限多的解。
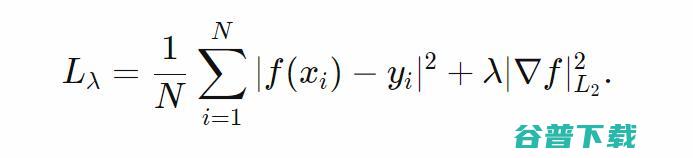
。我们并不想让方差为0，因为我们的正则化项仅仅是一个半范数）。当然了，Grace Wahba有关正则化回归的研究尤其与保持偏差-方差间的良好平衡相关，特别是与如何寻找到一个合适的值相关。
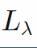
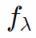
中将经验最小二乘损失(第一项) 最小化，就可以将前一节中的ansatz函数与嵌套空间Fi联系起来。因此来自递增权重序列
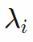
就给到了我们嵌套的Ansatz空间。
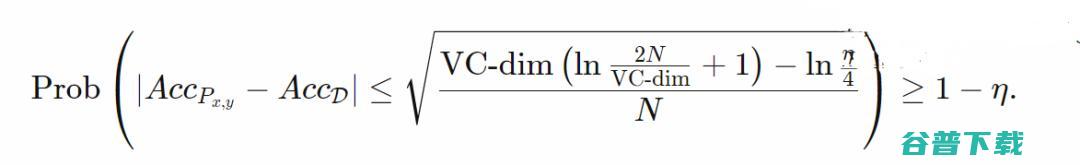
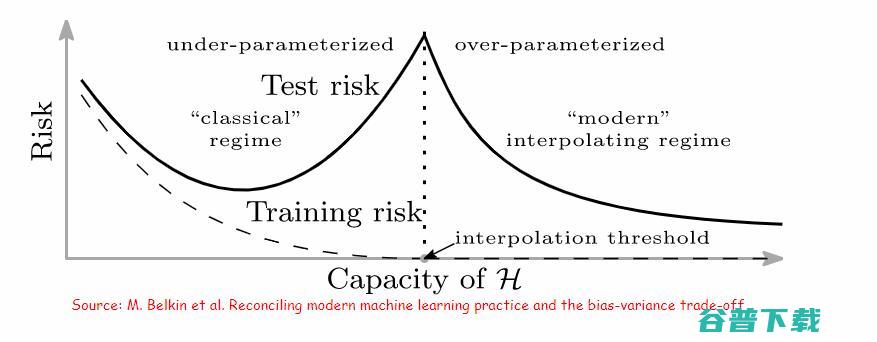
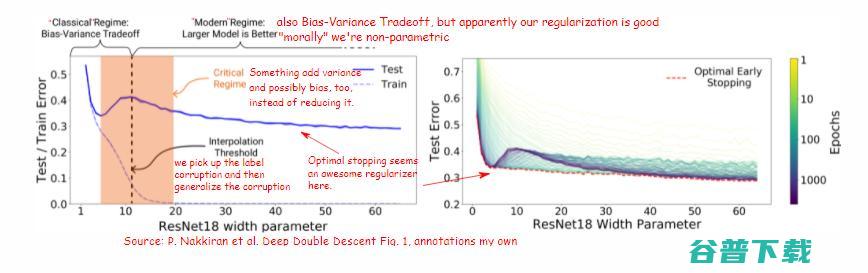
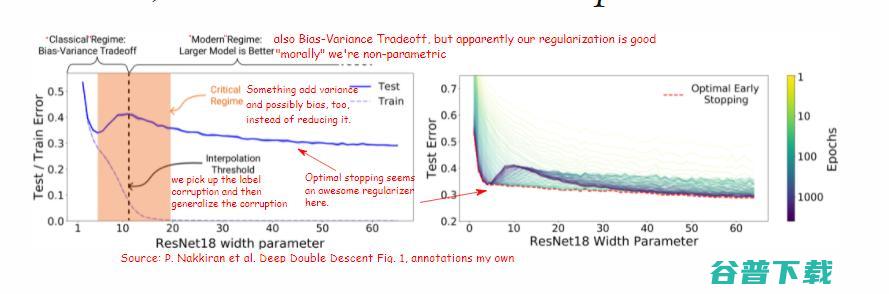
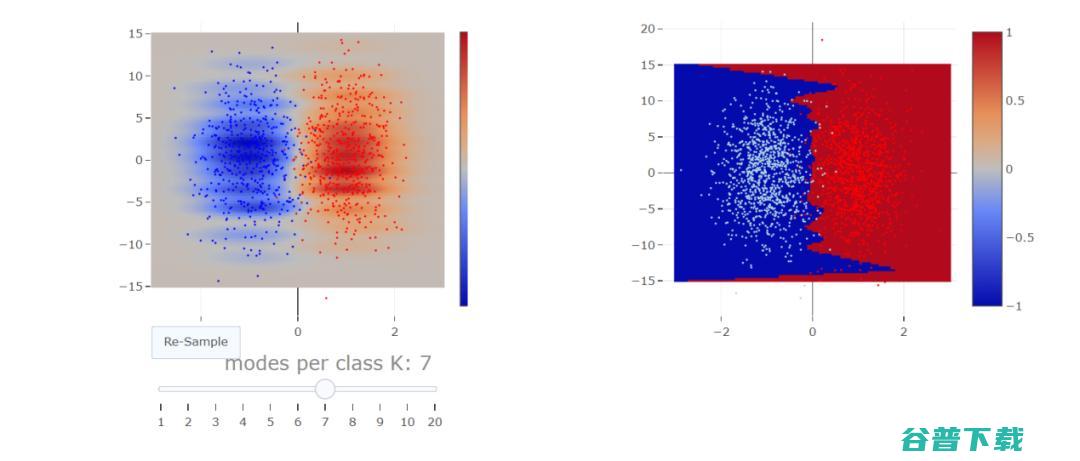
在插值条件中挤出错误标记的数据
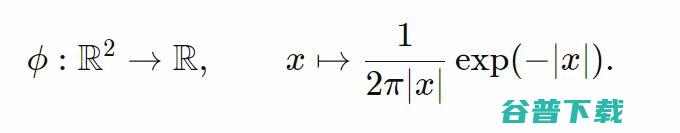
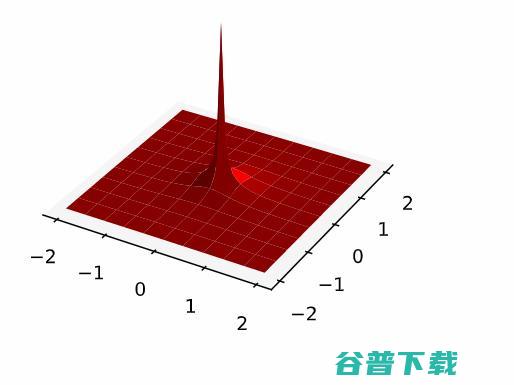
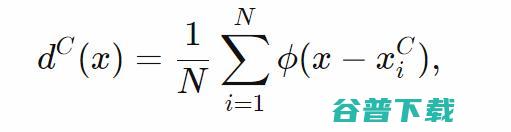
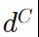更大的点对每个点进行分类，或者说，如果我们想通过标准化每个点的概率密度来获取概率
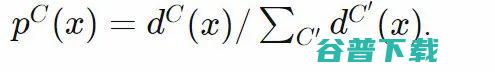
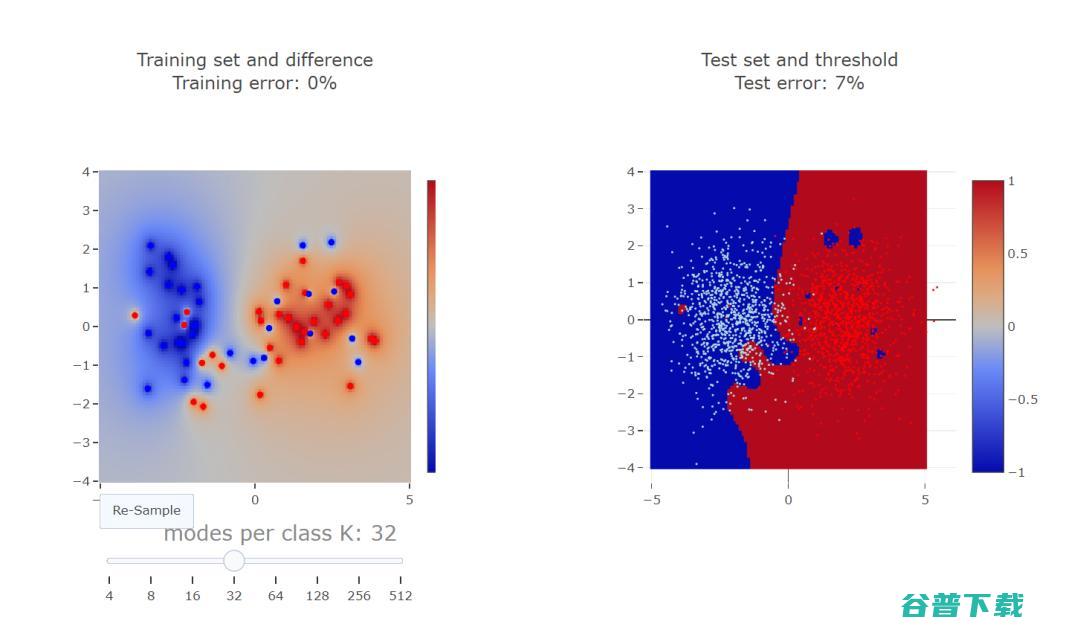
特征噪声类似于标签噪声
，当⋅+≥0时，类为1;否则，类为0。如果我们预先知道输入是有界的，我们可以找到类原型
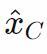
进行分类。但随后的线性分类器的−1维零空间(null-space)中的向量，比如我们可以添加到输入中而不改变结果的向量空间
，可能对这个距离有很大帮助，从而使得
成为对更相关的投影距离
版权文章，未经授权禁止转载。详情见 转载须知 。
华为云提供稳定可靠、安全可信、可持续发展的云服务，致力于让云无处不在，让智能无所不及，共建智能世界云底座。助力企业降本增效，全球300万客户的共同选择。7x24小时专业服务支持，5天内无理由退订，免费快速备案。
南京软服是一家专业从事南京建筑实名制、南京工地实名制系统、南京e路筑福实名制平台对接、南京二道门系统、南京化工厂人员定位系统、南京食堂打卡机消费机、南京门禁考勤机
X-MOL学术平台，顶级期刊论文图文内容每日更新，海内外课题组信息，行业新闻文摘，化学类网址导航，化学软件和数据库导航，及更多其他内容
杭州成人教育网提供：浙江工业大学、浙江工商大学、浙江科技学院等大学高起专、高起本、专升本、零基础升专科、零基础升本科，近百个热门专业的夜大函授远程学历。
上海科利瑞克是一家**方解石磨粉机的机械厂家,方解石磨粉机型号有很多,包括方解石超细磨粉机,方解石微粉磨,方解石三环中速磨粉机等,产品型号齐全,价格实惠,性价比高,获得了用户的一致好评.
瑞安市豪兴机械有限公司是一家集科研开发、制造、销售、服务为一体的现代化民营企业，具有多年开发生产信封纸袋机系列、贴窗系列的技术和经验。
安徽雨润仪表电缆有限公司是一家生产、销售、研发为一体的综合性仪表、电缆生产厂家。
成都家装设计公司里林设计工作室专注于家庭装修设计及施工,想了解成都性价比口碑装修哪家好点,成都装修公司排名哪家好,成都十大设计工作室排名，成都装修设计工作室q,成都家装公司哪些口碑比较好,成都市装修公司排名榜!
中山市豪宇机电有限公司专业生产高频焊机、高频钎焊机、手持式高频焊机、超音频退火机、超高频淬火机、中频熔炼炉、中频锻造炉等，技术工艺精湛、价格实惠，欢迎广大客户朋友前来参观选购。联系电话：13680141789杨小姐。
主要设备包括：矿山机械，工程机械装备，挖改潜孔钻机，钻孔爆裂一体机，挖掘凿岩机。
ozon/WB跨境电商行业资讯干货学习工具导航平台
油浸式变压器厂(德润变压器13806350849)生产(S11,S13,S20,S22)油浸式变压器,SZ11/110KV变压器,KS11矿用变压器,KS13矿用变压器,KSG矿用干式变压器,KBSG矿用防爆变压器,KBSGZY矿用防爆变压器,S11变压器,S13变压器油浸式变压器生产厂家是一家国营老厂,实力雄厚,产品均已通过国家权威试验机构检测
雷锋网消息，11月5日，赶在双十一到来之前，小米举行了一场堪称重磅的产品发布会，发布的产品包括小米CC9Pro智能手机，小米电视5Pro，小米智能手表——尤其是小米CC9Pro，它凭借1亿像素分辨率的相机配置引起了大量的关注，下午两点钟，发布会正式开始，小米CC9Pro，1亿像素拍照机皇小米CC9Pro最令人印象深刻的标签是，全球首款...。
单飞后的小冰，再次与微软结缘！11月24日上午9点，微软中国与小冰在北京举办联合发布会，宣布双方达成战略合作，将共同致力于为广大ToB重点行业客户，推出一系列人工智能，云计算商业化解决方案，小冰公司董事长，原微软全球执行副总裁沈向洋博士表示，仅四个月之后，小冰的商业化之路又迈出了坚实的一步，7月13日，为加快小冰产品线本土创新步伐，促...。
民航客机的驾驶舱如果在高空巡航状态下玻璃脱落，会对飞机和乘客的安全造成极大的影响，在一万米的高空上，空中的温度会比地面上温度低很多，气压可能只有正常标准气压的十分之三而已，含氧量更是极低的，正常人在海拔三千多米不到四千米的高峰上就已经无法正常呼吸了，更加是不用说是近万米以上的高空中的含氧量了，不知道大家有没有想象过，要是在万米高空中，...。
1、把当贝市场软件安装包，https，dlap1.dbkan.com，update，2024，08，12，dangbeimarket，5.0.6，312，znds.apk，下载并拷贝到U盘中，2、将U盘连接天猫魔盒8AirPro的USB接口，等待检测到外接设备，选择，应用，，找到当贝市场apk，点击并确认安装即可；注，如果没有弹出...。
2023年是最艰难的一年，受国际大环境影响，日本东芝33家工厂紧急撤离中国，搬往越南，导致40万人失业，上海深圳东莞60万人找不到工作，苹果代加工东莞钱大五金接不到订单，三家工厂倒闭，12万人面临失业，全国460万家工厂没订单，哀嚎一片，中国历史上最大的失业潮有可能来了，东芝紧急撤离中国33家工厂搬往越难，富士康、华硕、世硕、昌硕、立...。
[文，观察者网齐倩]查尔斯·利伯，CharlesLieber，现年65岁，是美国顶尖化学家和纳米迷信家、哈佛大学化学与化在校动物系前主任，但却因与中国高校协作，在2020年被卷入美国臭名昭著的，中国执行方案，，2021年12月被判有罪，后于2023年被判幽禁，去年，利伯从哈佛大学退休，据香港，南华早报，8月24日报道，此前有信息称，利...。
申明，1.以上内容仅代表揭发者自己，不代表黑猫揭发立场，2.未经授权，本平台案例制止任何转载，违者将被清查法律责任，3.黑猫揭发处置揭发不收取任何费用，凡以黑猫揭发名义不要钱的均为混充、诈骗行为，请及时报警并与黑猫官网反应，揭发邮箱heimaotousu@vip.sina.com，4.请大家选用官网渠道处置生产纠纷，不要轻信第三方机构...。
苹果手机下载微信的详细操作如下，工具，苹果手机，1、首先关上苹果手机，点击进入Appstore程序，2、进入Appstore程序后，在软件上面的搜查主要词栏中输入，微信，3、点击Appstore程序搜查结果中的选中的要下载的微信选项，4、在咱们选用的微信程序后点击右侧的下载按钮，5、点击下载按钮后稍微等一会，直到产生关上按钮，6、产...。
梦见放炮，预示着做梦人的好友运回升，人际相关将会越来越好，有新的想法和创意会有听众，可以分享给他们，梦见放鞭炮，预示着在新的一年里，自己可以收获到很多的喜气气，在新的一年里，自己的生存会有很大的扭转，自己在新的一年里会取得很多的喜气，这也是善报一桩，在梦中的自己，会遭到家人的关心，和家人之间的相关都会变得很好，也会有很多的礼物，能够收...。
[全球时报综合报道]，华尔街日报，2日颁布所谓，独家信息，称，美国智库策略与国际疑问钻研核心，CSIS，1日颁布的报告显示，卫星图像发现古巴正在树立一个新的雷达站，或者监听左近的关塔那摩湾美国海军基地，从而协助中国启动，特务优惠，相似的炒作，之前美国媒体已传出屡次，关于美国智库的新说法，古巴副外长和中国外交部发言人均予以批驳，华尔...。
用小兵一键重装WIN764位MSDN版没有网卡驱动怎么办？
uuRadio网络收音机,uuRadio为您提供简单方便的收听网络电台方式。内设100多个热门电台，你也可以添加自己喜欢的电台。电台数量不在多，只要有自己喜欢的电台就可以。,您可以免费下载。
在CES2021展会期间，Reasonance推出了一套，无绳电视，解决方案，推出了一款40英寸的，无绳电视，，并进行了展示，Reasonance直接将接收线圈安置在后面板上，利用了经典的，高级磁共振，原理，可兼顾功率、能效、传输距离和设计自由度，Reasonance是一项全新的技术，发射系统水平放置，与接收圈形成90°直角，最佳距离...。
中西文化结合之后，西式美食快速的进入到中国市场，凭借着产品的美味，以及鲜美的口感，赢得无数消费者的追捧，市场上不断的涌现出很多西式美食品牌，比如就有佐樱禾，这个品牌发展多年时间，一直坚持手切、绿色、健康的产品生产，留住更多的回头客，看到店铺生意十分红火，也让人们心中产生疑问，佐樱禾适合小孩去吃吗，佐樱禾创立于2017年，来自青岛，是一...。
服务对于考察幼儿园加盟机构来说，是不容忽视的一个环节，也是园长们普遍关注的部分，在目前市场上的加盟品牌中，香港跨世纪国际教育集团作为高端幼儿园加盟的引路者成为大热的幼儿园加盟品牌，香港跨世纪国际教育集团有27年的的品牌发展史，加盟园雄踞全国各地，它都有哪些服务呢，小编一起带您看一下，2、线下教学研发培训培养专业蒙氏老师3、进园指导、电...。
酸奶是以新鲜的牛奶为原料，经过巴氏杀菌后再向牛奶中添加有益菌，发酵剂，，经发酵后，再冷却灌装的一种牛奶制品，目前市场上酸奶制品多以凝固型、搅拌型和添加各种果汁果酱等辅料的果味型为多，酸奶不但保留了牛奶的所有优点，而且某些方面经加工过程还扬长避短，成为更加适合于人类的营养保健品，...。
发表在综合交流大区2022，7，2016，25刚听完周杰伦的新专辑是不是觉得还不过瘾，刘德华带着他的重映演唱会又来啦！！2022年刘德华MyLoveWorldTour演唱会重映将在7月22日首播；此前因为身体原因，刘德华的演唱会延期了很久，这次今年华哥的粉丝们又可以在线观看这场演唱会盛宴了，下面给大家分享如何用投影仪来观看刘德华演唱会...。
